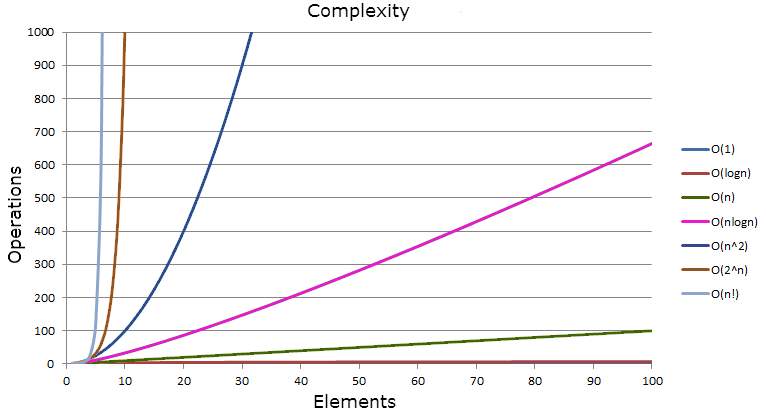
Big O

Notes from Cracking the Coding Interview - 6th Edition

• Time & Space Complexity

• Drop the Non-Dominant Terms

  • ${O(N^2 + N)}$ becomes $O(N^2)$

  • $O(N + log N)$becomes $O(N)$

  • $O(5*2^N + 1000N^{100})$becomes $O(2^N)$

• Multi-Part Algorithms: Add vs Multiply

  • ADD $O(A + B)$

  for (int a : arrA) {
      print(a);
  }
  for (int b : arrB) {
      print(b);
  }

  • MULTIPLY $O(A * B)$

  for (int a : arrA) {
      for (int b : arrB) {
          print(a + "," + b);
      }
  }

• Amortized Time

  $X$adds takes $O(X)$time. The amortized time for each adding is $O(1)$.

• Log N Runtimes

  • binary search example:

  search 9 within (1, 5, 8, 9, 11, 13, 15, 19, 21)
      compare 9 to 11 -> smaller
      search 9 within {1, 5, 8, 9}
          compare 9 to 8 -> bigger
          search 9 within {9}
              compare 9 to 9
              return

  With each comparison, we go either left or right. Half the nodes are on each side, so we cut the problem space in half each time.

• Recursive Runtime

  int f(int n) {
      if (n <= 1) {
          return 1;
      }
      return f(n - 1) + f(n - 1);
  }

  Remember pattern: when you have a recursive function that makes multiple calls, the runtime will ofter look like $O(branches^{depth})$, where branches is the number of times each recursive call branches. In this case, this gives us $O(2^N)$.

N	Level	#Nodes	Also expressed as...	Or...
4	0	1		$2^0$
3	1	2	2 * previous level = 2	$2^1$
2	2	4	2 * previous level = $2 * 2^1 = 2^2$	$2^2$
1	3	8	2 * previous level = $2 * 2^2 = 2^3$	$2^3$

• Sorting string takes $O(N log N)$

Examples

$O(N)$

void f(int[] array){
    int sum = 0;
    int product = 1;
    for (int i = 0; i < array.length; i++){
        sum += array[i];
    }
    for (int i = 0; i < array.length; i++){
        product *= array[i];
    }   
    System.out.printIn(sum + ", " + product); 
}

$O(N^2)$

void printPairs(int[] array){
    for (int i = 0; i < array.length; i++){
        for (int j = 0; j < array.length; j++){
            System.out.printIn(array[i] + ", " + array[j]); 
        }
    }
}

$O(N^2)$

Important to note here is line 3 in the code: int j = i + 1 (see page 46/47)

void printUnorderedPairs(int[] array){
    for (int i = 0; i < array.length; i++){
        for (int j = i + 1; j < array.length; j++){
            System.out.printIn(array[i] + ", " + array[j]); 
        }
    }
}

$O(ab)$

void printUnorderedPairs(int[] arrayA, int[] arrayB){
    for (int i = 0; i < arrayA.length; i++){
        for (int j = 0; j < arrayB.length; j++){
            if (arrayA[i] < arrayB[j]):
                System.out.printIn(arrayA[i] + ", " + arrayB[j]); 
            }
        }
    }
}

$O(ab)$

The most inner for loop is considered as a constant -> 100,000 units.

void printUnorderedPairs(int[] arrayA, int[] arrayB){
    for (int i = 0; i < arrayA.length; i++){
        for (int j = 0; j < arrayB.length; j++){
            for (int k = 0; k < 100000; k++):
                System.out.printIn(arrayA[i] + ", " + arrayB[j]); 
            }
        }
    }
}

$O(N)$

void reverse(int[] array){
    for (int i = 0; i < array.length / 2; i++) {
        int other = array.length - i - 1;
        int temp = array[i[;
        array[i] = array[other];
        array[other] = temp;
    }
}

$O(N)$

Balanced binary search tree (see page 49).

int sum(Node node){
    if (node == null){
        return 0;
    }
    return sum(node.left) + node.value + sum(node.right);
}

$O(\sqrt{n})$

boolean isPrime(int n){
    for (int x = 2; x * x <= n; x++){
        if (n % x == 0){
            return false;
        }
    }
    return true;
}